LeetCode 二叉搜索树与双向链表

题目描述

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点，只能调整树中节点指针的指向。

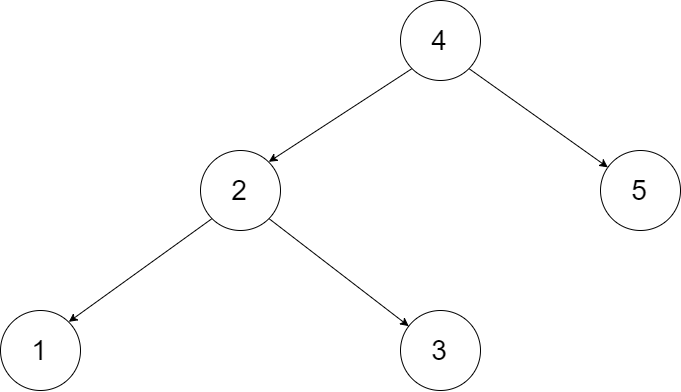
为了让您更好地理解问题，以下面的二叉搜索树为例：

我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表，第一个节点的前驱是最后一个节点，最后一个节点的后继是第一个节点。

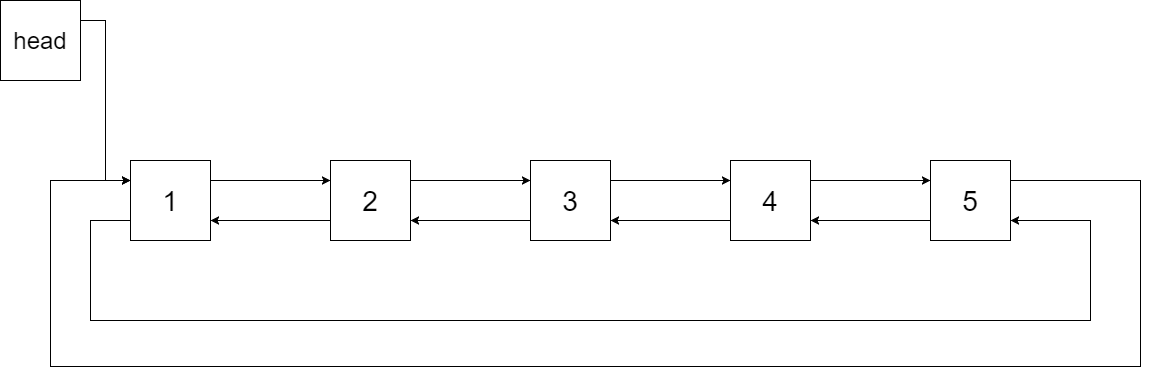
下图展示了上面的二叉搜索树转化成的链表。“head” 表示指向链表中有最小元素的节点

特别地，我们希望可以就地完成转换操作。当转化完成以后，树中节点的左指针需要指向前驱，树中节点的右指针需要指向后继。还需要返回链表中的第一个节点的指针。

解题想法

题目给出的是一棵二叉搜索树，而要我们整理成一个升序的双向链表，可以很自然的想到二叉搜索树的中序遍历即为升序序列。面对双向链表，我们还需要建立相邻结点之间的关系，因此需要设置前驱结点pre和当前结点cur两个指针来组织结点之间的关系。（具体即为pre->right = cur和cur->left = pre），最后则是连接头结点和尾结点。

中序遍历流程

令recur为中序遍历函数

1、终止条件：当cur结点为空时，直接返回，说明此时已经越过了叶节点

2、递归左子树，recur（cur->left）

3、构建相邻结点之间的关系

（a）、如果pre指针为空，说明当前访问的结点为中序遍历的第一个结点，也就是双向链表的头结点，此时将当前结点cur赋值给head指针。

（b）、如果pre指针非空，需要建立两个结点之间的关系，即pre->right = cur和cur->left = pre

（c）、更新前驱结点pre，即pre = cur

4、递归右子树，recur（cur->right）

最后在执行函数中，需要利用head和pre指针建立双向链表的头尾关系，即head->left = pre，pre->right = head，因为当递归完二叉搜索树时，pre会指向中序的最后一个元素。

代码

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* left;
    Node* right;

    Node() {}

    Node(int _val) {
        val = _val;
        left = NULL;
        right = NULL;
    }

    Node(int _val, Node* _left, Node* _right) {
        val = _val;
        left = _left;
        right = _right;
    }
};
*/
class Solution {
private:
    Node *head, *pre;
    void recur(Node *root) {
        if (root == NULL) return;
        recur(root->left);
        // 如果pre为空，说明当前访问的是头结点
        if (pre) pre->right = root;
        else head = root;
        root->left = pre;
        // 修改当前的结点为前驱结点
        pre = root;
        recur(root->right);
    }
public:
    Node* treeToDoublyList(Node* root) {
        if (root == NULL) return NULL;
        recur(root);
        head->left = pre;
        pre->right = head;
        return head;
    }
};